<<1−3 回路の要素へ
1−4 基本的な回路1
回路の基本動作を紹介する。
ここでは、回路の基本動作を理解しやすいようにあくまで理想回路であり、回路図どおりの要素しかないものとしている。
実際の回路では、理想回路とは違う点が色々出てくる。その点は4章にて掲載する予定である。
a.直流回路
電気回路で最も基本的な回路は、下記のような電源と抵抗だけの回路である。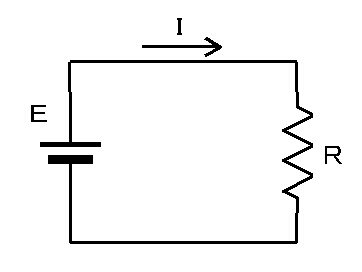 |
| <図−1.4.1>抵抗のみの基本回路 |
この回路での電流Iは、
I=E/R [A]
で求められる。
また、抵抗に電流を流すと、熱として電力を消費する。
この時消費する電力Pは、
P=I・E=E2/R [W]
で求められる。
※消費電力は直流の場合、抵抗にかかわらず、素子の両端の電圧と素子に流れる電流を掛ければ求めることができる。
実際の回路で使用する部品には、許容されている電力が決まっているため、その部品の定格電力以内で使用するよう注意する必要がある。
・抵抗を直列に接続した場合の考え方
 |
| <図−1.4.1a>抵抗を直列にした場合 |
抵抗を直列に接続した場合、それぞれの抵抗に流れる電流は同じである。
これより、それぞれの抵抗にかかる電圧は、
VR1=I・R1 [V]
VR2=I・R2 [V]
これより、抵抗に流れる電流は、
I=E/(R1+R2) [A]
で求められる。
よって、抵抗を直列に接続した場合は、それぞれの抵抗値を合計したものが全体の抵抗値となる。
全体の抵抗値Rは
R=R1+R2 [Ω]
となる。
・抵抗を並列に接続した場合の考え方
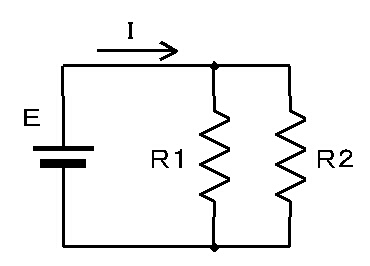 |
| <図−1.4.1b>抵抗を並列にした場合 |
抵抗を並列に接続した場合、それぞれの抵抗にかかる電圧は同じである。
これより、それぞれの抵抗に流れる電流は、
IR1=E/R1 [A]
IR2=E/R2 [A]
これより、抵抗に流れる電流の合計は、
I=IR1+IR2=E(1/R1+1/R2)=E・(R1+R2)/R1・R2 [A]
となる。
これより抵抗を並列に接続した場合は、それぞれの抵抗値の逆数の和の逆数が全体の抵抗値となる。
全体の抵抗値Rは、
R=1/(1/R1+1/R2)=R1・R2/(R1+R2) [Ω]
となる。
b.直流回路の過渡現象
コンデンサやコイルは、直流で定常状態(電圧・電流に変化がない状態)においては、抵抗は∞や0である。しかし、電圧の変動があるとこれとは異なった特性を示す。このとき生じる現象を過渡現象という。
以下に過渡現象の基本を説明する。
i.R−C回路
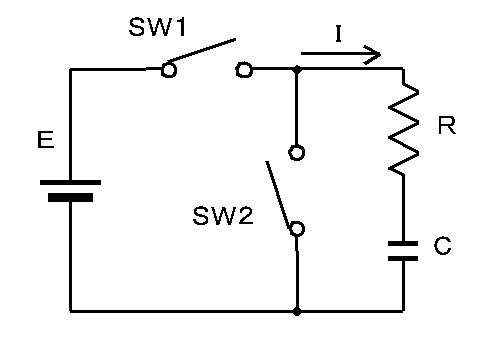 |
| <図−1.4.2>R−C回路 |
コンデンサは、電圧が一定であると電流は流さない(抵抗値は∞)が、上記回路のSW1をONにすると、電流が流れる。
コンデンサには、(変化した分の電圧x静電容量)分の電荷が蓄えられるまで電流が流れる。
このとき流れる電流は、
v(t)=R・i(t)+1/C・∫i(t)dt
の微分方程式の解より、
SW1をONにしてt秒後の電流iは、
i(t)=E/R・e(-t/RC) [A]
となる。
SW1をONにした直後は、Cはショート状態と同じであり、電荷がたまってくるにつれて電流が減少していく。
この関係をグラフに表すと下図のようになる。
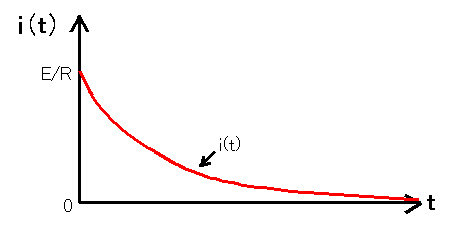 |
| <図−1.4.3a>コンデンサに流れる電流の変化 |
また、コンデンサにかかる電圧vcは、
vc(t)=E(1−e(-t/RC)) [V]
となり、この電圧の変化をクラブにすると、下図のようになる。
 |
| <図−1.4.3b>コンデンサにかかる電圧の変化 |
SW1を十分な時間ONにしてコンデンサを完全に充電した後、SW1をOFFしSW2をONにするとコンデンサから電流が流れ出す。
この時の電流iは、
i(t)=E/R・e(-t/RC) [A]
となり、コンデンサの電圧vc(=抵抗両端の電圧)は、
vc(t)=E・e(-t/RC) [V]
となる。
ii.R−L回路
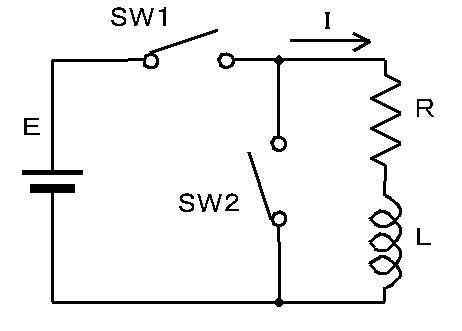 |
| <図−1.4.4>R−L回路 |
コイルは、電流が一定であると、抵抗は0と同じであるが、上記回路のSW1をONにすると、コイルに生じる逆起電力のため始めは電流が流れない。
時間が経つにつれて電流は大きくなる。
この時の電流は、
v(t)=Ri(t)+L・di(t)/dt
の微分方程式の解より、
SW1をONにしてt秒後の電流iは、
i(t)=E/R・(1−e(R/L・t))
となる。
SW1をONにした直後は、コイルに流れる電流iは0になり、電流が増加し最終的には電流はE/Rまで増加する。
この関係をグラフに表すと下図のようになる。
 |
| <図−1.4.5>コイルに流れる電流の変化 |
c.交流回路
交流回路では、抵抗は直流回路と同じ働きをする反面、コイルやコンデンサは異なる働きをする。i.交流回路でのコイルの働き
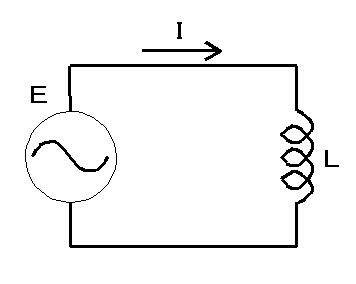 |
| <図−1.4.6>コイルのみの回路 |
上図のようにコイルに交流電圧を加えるとコイルに電流が流れるが、コイル自体では電力は消費しない(熱として消費しない)。
このときにコイルに流れる電流を無効電流といい、エネルギーとして消費されることなく電源へ帰っていく電流である。
また、このときの電流と電源電圧を掛けたものを無効電力という。
この時に流れる電流は、下図のように電源電圧に対して位相が90°遅れたものになる。
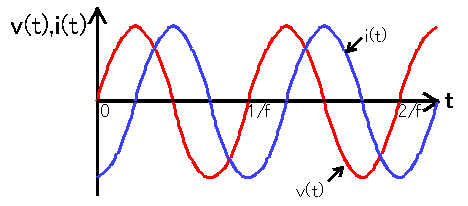 |
| <図−1.4.7>コイルのみの場合の電流と電圧の位相 |
※インピーダンスについて
交流での抵抗(電流の流れにくさ)に相当するものをインピーダンス[Impedance]という。単位は同じ[Ω]である。
直流の抵抗と異なるのは、インピーダンスには、虚数部が存在することである。
複素数の形を用いることにより、無効電流を含めた計算を容易に行うようにしている。
コイルのインピーダンスZは、
Z=jωL [Ω] j=√(−1),ω=2πf
となる。
コイルに流れる電流iは、
I=E/Z=E/jωL=−j(E/ωL) [A]
となる。
このようにコイルは周波数fによりインピーダンスが変化する。
周波数が高くなればインピーダンスは大きくなり、コイルに流れる電流は減少する。
ii.交流回路でのコンデンサの働き
 |
| <図−1.4.8>コンデンサのみの回路 |
上図の場合ではコンデンサもコイルと同様に無効電流のみ流れる。
この時の電流は、電源電圧に対して位相が90°進んだものになる。
 |
| <図−1.4.9>コンデンサのみの場合の電流と電圧の位相 |
コンデンサのインピーダンスZは、
Z=1/jωC=−j/ωC [Ω]
となる。
コンデンサに流れる電流iは、
I=E/Z=j(E・ωC) [A]
となる。
このようにコンデンサは周波数fによりインピーダンスが変化する。
周波数が高くなればインピーダンスは低くなり、コンデンサに流れる電流は増加する。
iii.R−L直列回路
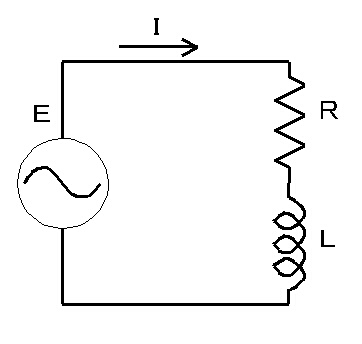 |
| <図−1.4.10>R−L直列回路 |
今度は、上図のようにコイルと抵抗を直列に接続した回路を考えてみる。
この場合のインピーダンスZは、
Z=R+jωL [Ω]
となる。
電流はIは、
I=E/Z=E/(R+jωL) [A]
となる。
有効電流、無効電流を合計した、電流の絶対値|I|は、
|I|=E/√(R2+ω2L2)
となる。
グラフにすると、下図のようになる。
 |
| <図−1.4.11>R−L直列回路の周波数特性 |
電流(または電圧)が電流(または電圧)の最大値の1/√2(≒−3dB)になる周波数、カットオフ周波数fcを求めてみると、
|Ifc|=1/√2・E/R=E/√(R2+ω2L2)
より、
fc=R/2πL [Hz]
となる。
※絶対値について
電気回路を設計するときは、Z=R+jXという形では分かりづらいため、絶対値|Z|を用いる。
絶対値は、実部の自乗と虚部の自乗を足したものの平方根。
|Z|=√(R2+X2)
iv.R−C直列回路
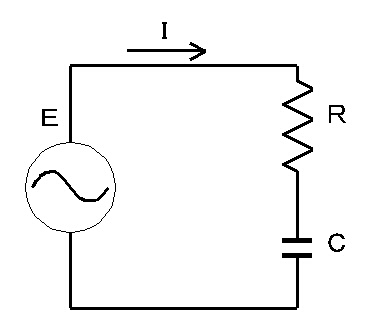 |
| <図−1.4.12>R−C直列回路 |
コンデンサと抵抗を組み合わせた場合は、インピーダンスZは、
Z=R−j・1/ωC [Ω]
となる。
電流Iは、
I=E/Z=E/(R−j・1/ωC)
=(ω2C2R+jωC)/(1+ω2C2R2)・E[A]
となる。
電流の絶対値|I|は、
|I|=(√((ω2C2R)2+(ωC)2))/(1+ω2C2R2)
=ωC/(√(1+ω2C2R2))・E [A]
となる。
グラフにすると、下図のようになる。
 |
| <図−1.4.13>R−C直列回路の周波数特性 |
カットオフ周波数fcは、
|Ifc|=1/√2・E/R=ωC/√(1+ω2C2R2)・E [A]
より、
fc=1/2πCR [Hz]
となる。
v.R−L−C直列回路
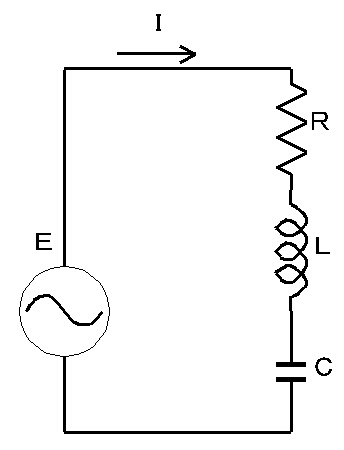 |
| <図−1.4.14>R−L−C直列回路 |
抵抗・コイル・コンデンサを直列に組み合わせた回路の場合、
Z=R+j(ωL−1/ωC) [Ω]
となり、これより、
I=E/(R+j(ωL−1/ωC)) [A]
となる。
この式から分かるように、ωL=1/ωCとなると、インピーダンスはRだけとなり最も小さくなる。
この条件を直列共振といい、この条件になる周波数を共振周波数という。
 |
| <図−1.4.15>R−L−C回路の周波数特性 |
共振周波数f0は、
ωL=1/ωCより、
f0=1/(2π√(LC)) [Hz]
となる。
vi.L−C並列回路
 |
| <図−1.4.16>L−C並列回路 |
コイルとコンデンサが並列に接続された場合は、コイルのインピーダンスをZL、コンデンサのインピーダンスをZcとすると、
Z=1/(1/ZL)+(1/Zc))
=j・1/(1/ωL−ωC) [Ω]
I=j(ωC−1/ωL)・E [A]
となる。
この式より、ωC=1/ωLになると、インピーダンスZは∞になり、電流Iは0となる。
この条件を並列共振という。
このときの共振周波数f0は、
ωC=1/ωLより、
f0=1/(2π√(LC)) [Hz]
となる。
 |
| <図−1.4.17>L−C並列回路の周波数特性 |
>>1−5 基本的な回路2へ